I collect here some of the notes of the lecture on Algebra I followed in the3rd_Semester at theLMU held by A. Rosenschon.
Recap
Elementary Group Theory
Most of theorems of this section were present already in Linear Algebra II (Lecture).
- Normal Divisor
- for subgr., ,
- , , ,
- (Lagrange)
- for subgr.,
- Ways to prove :
- for ,
- , link.
- is a gr.autom.
- for subgr., ,
- Homomorphism and Isomorphism Theorems 1.12
- for (i) hom., (ii) s.t. , (iii) then:
ex. uniq. s.t. G \to^\pi G/N \to^\overline{\varphi} G', groups_hom.png
- surj, then is isom.
- subgr. , then (i) subgr., (ii) , (iii) , (iv) (1st Isomorphism Theorem)
- for , , then (i) , (ii) , (iii) (2nd)
- for (i) hom., (ii) s.t. , (iii) then:
ex. uniq. s.t. G \to^\pi G/N \to^\overline{\varphi} G', groups_hom.png
- Grothendieck
- Cyclical Groups
- ...
Rings and Polynomials
Most of these theorems are present in Linear Algebra II (Lecture) already, though I list some of them here again:
- for hom, inj. surj. No, find the right version
- for comm, (B.9.1.a)
- Rings and Polynomial Rings in one Variable
- def. of Ring: for a group with and a monoid with it holds and . It is comm. if .
- if , then
- , is a group.
- For a family of rings, is ring with component-wise and .
-
- with and from . 2.2-2.3
-
- , .
- def. of Ring: for a group with and a monoid with it holds and . It is comm. if .
- Ideal
- def. ideal s.t. subgroup of and
- def. generator , if , fin.gen. if , principle if .
- 2.14: prime Ideal if , max. ideal if all ideals , .
- 2.15: comm., prime iff is ID. max. ideal is a field.
- for max., I prime. max. prime.
- Rings-homomorphisms and Factor-rings
- def hom. s.t. (i) , (ii) , (iii) .
- is an ideal, is a subr., determines a gr. hom. . inj.
- Homomorphiesatz
- Chinese Restsatz
- def hom. s.t. (i) , (ii) , (iii) .
- Prime Factorisation
- def. let s.t. , there is s.t. where , then is eucl. ring and a norm. 2.17
- eucl PID
- irr. if
- prime if
- (i) max. prime, (ii) prime irr. (iii) PID: irr. prime max. 2.20
- PID, , then . unique up to order and mult. with units. 2.22
- def Fact. Ring: if (i) or (ii) irr elem. 2.23
- Fact. Ring prime irr.
- eucl. PID Fact Ring
- ,
- in an there could be no bc not every ideal is principal. 2.26
- for is PID, is a field, link.
- PID is a filed, link.
- pr. ideal ID (B.9.1.c)
- max. ideal is a field. (B.7.1.a)
- Roots of Polynomials
- a field then has max. roots, exactly if .
- , , then mult. root .
- , , with the fraction operation define the the quotient field, called . 2.28 Also .
- , (Gauss-lemma) fact. Ring .
- (Gauss) fact. fact.: pr. pr. primitive in prime in .
- fact. primitive in : irr in irr. in .
- for , , link.
- is the for all coefficients of ., wiki.
- Irreducibility Criteria for fac. ring with quotientfield and primitive.
- (Eisenstein) primitive, and there is prime in , s.t. , , , then irr. in . 2.34
- (Red. mod. ) , s.t. and for . If irr. then irr in Q(R)[X], if also primitive, then irr. in . 2.35
- Methods (Sol. 9.2): for fac., , ., check red. of in
- Eisenstein: check for all s.t. , if it works, it is irr., else continue
- Roots: check poss. roots in , i.e. s.t. , , , if none, continue
- Degree: if , has no roots irr. (if no roots, conclude)
- Reduction: if , , then irr. irr., try further red.., else continue
- recall irr. pol. of in (link): for , try , else
- and for
- recall irr. pol. of in (link): for , try , else
- Absurdum: if , norm., no roots, try get cont., else
- , with roots , if , irr.
- irr. irr. (Wiederholungsblatt 6.a, Tut.B.9-10)
- is with the order of the coefficients inverted, this can help to apply Eisenstein.
Algebraic Field Extensions
- Characteristic
- def. for ID , for s.t. then .
- subr.
- def. prime field subfield, smallest subfield of .
- (i) , (ii) .
- (iii) any field contains some or a up to isomorphism.
- (i) , (ii) .
- def. for ID , for s.t. then .
- Field-Extentions
- ext. if is a subfield of . Note that is a -VS.
-
- , algebraic on if ex. s.t. . alg. if all is alg.
- , alg. on iff .
- alg., ex! s.t. (i) norm., (ii) , then prime, min. of
- is the min. poly. of if it is normed, irr. and has as a root.
- All finite extensions are algebraic. 3.7
- alg. each subring , s.t. is a field B.6.4
- fi. for
- 3.9
- Method: find , for , min.pol. B.6.2.b
- , rewrite the equation in order to get
- , min of then , hence . 3.8
- fin.gen. if , simple if 3.10
- if s alg. in : (i) , (ii) finite (alg. + fin. gen = finite) 3.11
- , alg. on , alg.: (i) alg. on , (ii) alg. , alg. 3.12
- Method: , find deg. and basis, B.6.1
- guess the min.pol., it is normed, irr. and has as a root, repeat for each
- multiply the degrees and compute the basis: .
- guess the min.pol., it is normed, irr. and has as a root, repeat for each
- ,
- ext. if is a subfield of . Note that is a -VS.
- Algebraic Closure
- (Kronecker) for field and , there is s.t. .
- , then after less than steps is red in lin. fact. 3.14
- alg. cl. if all non-const have a root, i.e. , , 3.15
- alg. cl.
- alg. cl. ( alg. cl )
- each has an alg. closure . 3.17
- Let field, hom., min of , s.t. :
- (a):
- (b): for , , then s.t. is unique.
- 3.18
- For alg. ext. of , :
- (a): s.t. and exists
- (b): if alg. cl. and alg. then is an isom.
- If , alg. cl. and ext. of and , then ex. and is isom. 3.20
- also , wiki.
- (Kronecker) for field and , there is s.t. .
- Splitting Fields
- field, , is called spl.fi. if (i) any splits in lin. factors, (ii) roots of s. is then called normal.
- spl.fi. of is for s the roots fo . For more polynomials, let .
- (Compactness) let be spl.fi. of for , let and , . 3.31.iii
- Every two spl.fi. of the same polynomials are isomorphic.
- alg. ex. tfae:
- norm.
- irr. s.t. splits in lin. fact.
- defines a -autom. of .
- norm.
- normal closure of alg. ext. if (i) alg., (ii) norm., (iii) minimal. 3.25
- alg. then:
- unique up to isom normal closure
- finite finite
- if alg., norm. then ex. norm. cl. of s.t. , for -hom. . is unique as a subfi. of . 3.25
- alg. then:
- norm. (tut.13.5)
- Method: find the spl.fi. of :
- Roots: find the roots of , call them .
- Minimise: try to find the smallest set of roots s.t. contains all roots
- Methods: for spl.fi. for , find and compute B.9.3.b
- Roots: those are , for .
- Splitting field: then
- Degree: must divide if prime check
- Min. Pol.: irr., .
- compute , recall (for )
- Separable Field Extensions
- sep. if has no mult. root in
- is mult. root of
- irr. then not sep. in 3.26
- irr. sep.
- irr. sep., link, 3.27
- :
- not sep. ()
- (Frobenius) , inj., perf. aut.
- Defs: 3.28
- alg., sep. over if for sep.
- alg. is sep. if any sep. over .
- perfect if all alg. are sep., wiki
- (i) perf., (ii) perf. (iii) per. (iv) alg.ext. of per. is per.
- alg. sep.deg. is , for set of -hom. 3.30
- norm. , see Galois Theory.
- is -hom. if .
- , min of then 3.31
- sep. over
- if and mult. of in is , then
- alg. ext., 3.32
- sep.
- always:
- fin., then sep. for sep. over
- alg., let s.t. , then sep. any sep. over .
- if , alg. then sep. , sep. 3.35
- subgr. cycl.
- sep. if has no mult. root in
- Theorem of the Primitive Element: fin. sep. ext. . Also is primitive to .
- Finite Fields
- For , , ex. unique up to isom. s.t. .
- For is spli.fi. of
- holds, hence
- extensions are the only extensions of finite fields with char. .
- wiki.
- For , , ex. unique up to isom. s.t. .
Galois Theory
True love makes non-Galois couples: not normal or inseparable. And if you claim your lover to be perfect, be aware that they are separable to anyone.jokes
- is gal. norm. and sep., a gal. gr. , Galois Examples.
- normal, then:
- recall: norm. 3.23.c
- separable, then:
- ()
- gal.
- gal. fin. , for is uniq. def. by .
- , root ,
- , .
- gal., :
- (i) gal., subgr.
- (ii) if gal. is surj. hom.
- field, , then (fixkö. of ): 4.4
- (i) gal.
- (ii) alg. gal. subgr.
- norm.: 4.5
- (i) gal.
- (ii) if sep. then
- for , , then
- (Gal.-Cor.) gal., norm. ( gal.) 4.6
- if fin. sep. then
- if also norm.cl. then fin. gal. and .
- if fin. sep. then
- Method: find , spl.fi. of in , and all s.t.
- Galois Ext. is a spl.fi., hence is norm., prove it to be sep.
- sep.
- fin., then sep. for sep. over
- alg., let s.t. , then sep. any sep. over $K
- Degree: find , conclude
- Elements:
- let
- determine using that is a -automorphism.
- combine a fixed with any , and check wether they are automorphism
- Stop when are finished or you already got many automorphism.
- Isomorphic Class: check isomorphisms with the groups in the table using the listed methods
- Galois Correspondence: subfields of correspond to subgroups of
- for , are exactly the subfields
- to compute consider for the basis of and recall , for instance if \sigma(a + b \sqrt{2} + c \sqrt{3} + d \sqrt{6})$$= a - b\sqrt{2} + c \sqrt{3} + d\sqrt{6}, then .
- Galois Ext. is a spl.fi., hence is norm., prove it to be sep.
- normal, then:
- Roots of the Unit
- for for
- subgr. of , cycl. 4.9
- .
- if then hence sep. and .
- pr. if or equivalently .
- for pr. , is spl.fi. of
- if , , then sep., since , and share all roots. From now on assume .
- ,
- if then
- gen., of gen., of pr. (Euler--function)
- for
- for and pr. 4.11 (circ. div. pol.)
- for all , is irr.
- for , pr., ,
- ,
- , pr., then sep., spl.fi of , i.e. fin.gal. check note 4.13.
- for , , pr. then , also irr. 4.15 ?
- , primitive for , then (i) gal., (ii) , (iii) .
- call gal. abelian if is abelian. [[Algebra (Lecture)#example-with—zeta|Example with ]].
- for for
- Roots Extensions
- , is rad. if there are s.t. 4.18
- rad. fin.
- , rad. then ex. s.t. s.t. rad. gal. 4.20
- gal. rad., , then is quot. of a gr. s.t. (i). 4.21
- (i): exists subgr. s.t. , ab. ( solvable)
- , is sol. with rad. if ex. rad. with all roots of . 4.22
- sol.w.rad. quot.gr. of s.t. (i)
- solv.w.rad. is solv. (not proved)
- sol.w.rad. quot.gr. of s.t. (i)
- , is rad. if there are s.t. 4.18
Advanced Group Theory
- a set, the set of bij. on , is a gr. on , operates on if ex. hom.
- for , write , also
- , write .
- Within these two rules, can be freely chosen (similarly to the for a VS)
- oper. on roots of .
- oper. on , for def:
- (orbit of )
- (stabilisator of )
- subgr of , 5.3
- for , oper. on with 5.6.a
-
- (i) , (ii) ab. , (iii) , (iv)
- (), since bij. 5.5
- Tut.12.1.a
- obv.
- , for , then
- (orbit of )
- abel. 5.6.c
- , , a syl.--subgr of is s.t. , i.e. max. -subgr.
- , , then for any has a subgr s.t. (Syl.-I)
- for , has an elem. of order . (Special Theorem of Cauchy)
- , , (Syl.-II)
- for syl.--subgr. then
- the only syl.--subgr , (i.e. ).
- and (mod. ) (Syl. III)
- , , syl.-- subgr. of
- Method: prove there is no simple group of order , tut.B.13.1
- Sylow Subgruops: consider the factorisations of the from , ,
- Sylow III: for each , found above determine possible s.t. and .
- Absurdum: assume for each found in 1., assume and get contradiction
- Sylow II: since there is one s.t. , then use the only syl.--subgr .
- , and syl.subgr. of , , tut.B.13.2 (weaker transitivity)
- Classification of Groups of Small Order
- Abelian Groups
- (a) for an ab.gr. s.t. then ex.uniq. a partition , , s.t. .
- (b) for an ab.gr. s.t. , then .
- Groups through Generators and Relations
- is the gr. generated by s.t. .
- Questions are: (i) is one of the conditions redundant? (ii) is it a trivial gr.?
- for
- (gr. of symm. of an -sided reg. polygon)
- max. ord. of the first rotation is
- for equal or this is enough, for it might still be .
- the reflection has ord. .
- this information is not very helpful since there is such a in each possible group.
-
- this shall be checked for .
- recall is not abelian
- ,
- , , yt,
- to get (i.e. snd inverse for , i.e. )
- for , .
- prime, or . 5.19
- not ab., 5.20
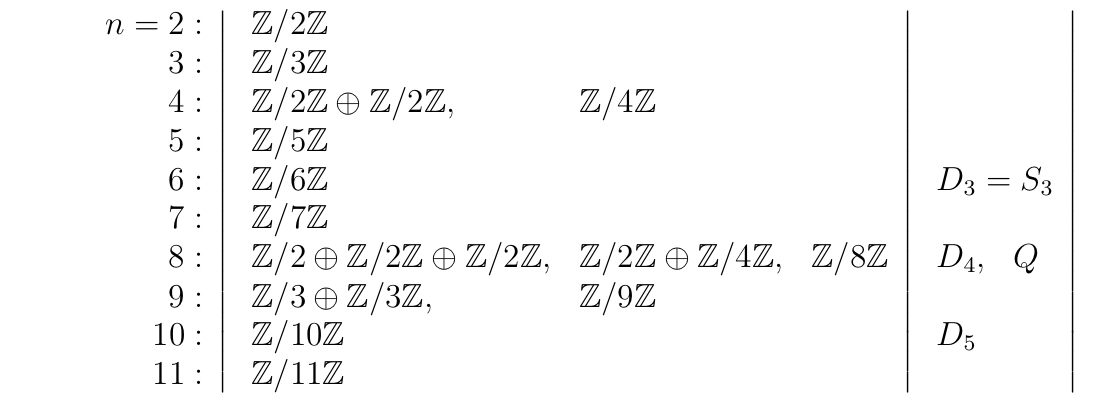
- is the gr. generated by s.t. .
- Abelian Groups
- Solvable Groups
- sol. if ex. s.t. (i) subgr., (ii) , (iii) ab.
- ab. sol. (, , ab.)
- For subgr., , then: 5.23
- sol. sol.
- sol. sol.
- sol. sol.
- sol. (Burnside)
- we only proved: sol. 5.24
- sol. (Feit-Thompson) (nor proved)
- sol. if ex. s.t. (i) subgr., (ii) , (iii) ab.
- Simple Groups
- sim. if i.e. there’s no non-trivial norm.div. 5.25
- sim.
- sim. 5.26
- not sol
- is smallest s.t. (i) not ab., (ii) sim.
- sim. if i.e. there’s no non-trivial norm.div. 5.25
Polynomials with as Galois Group
- for not sol. with rad.
- since permutes roots of , subrgr.
- since , not sol.
- for : 6.1
- (i)
- (ii) if ex. s.t. (iia) trans.subgr. and contains a transp. and -cycle, then
- for , ex. s.t. then trans subgr.
- , irr. s.t. and has exactly 2 not-real roots, then 6.2
- cycl.,
- if , ex. an elem. of order .
- for irr.,
- , is simple and separable (since is finite)
- if , ex. an elem. of order .
- fin. sep., if , is min. of , so irr. of deg. .
- irr..
- fac.ring., pr.ideal, , , . For primitive, let be , then: (i) sep sep., (ii) subgr. 6.4 (not proved)
Examples
For Galois Theory I decided to write down some of the examples too, I collect them here:
Galois Examples
- (a). , , since hence norm., sep. Also , elem. in premute roots () of , i.e. and (uniq. def. by s)
- (b). has zer. kö. , . is gal., . Elements perm. roots, (22:33, 2-2:33, 22:3-3, 2-2:3-3), .
- (c) , let s.t. , roots of is , is zer.kö. of , , prem. the roots, hence (smallest non-abelian), gal. gr. must not be abelian. The extension between, , , hence , hence , hence it is not a gal. ext.
- , , , , and sep. ( finite), (norm. zer.kö. for ) , see script for conclusion.
Galois Correspondence Examples
- (a) is gal. and as in Galois Examples (b). For the other examples, see the script.
Example with
- , prim. for , . , for . . Also note . Also has three non trivial fields in between: , , hence . The second field is: , , then . , similarly .